Matplotlib 绘制3D图像|极客笔记

前文学习了三维的坐标系，就可以建立起一个三维的环境，只需要简单地往里面装入数据，就可以显示三维图像出来，比如像下图：

Matplotlib 绘制3D图像

在这个图里，Z轴的坐标是从-2到2，X轴和Y轴都是-4PI到4PI，这是一个旋转的曲线，在X轴和Y轴里按圆的角度在变化，而半径是随着高度按抛物线来变化：r = z**2 + 1。因此构造三个坐标轴的数据代码如下：

theta = np.linspace(-4 * np.pi, 4 * np.pi, 100)
z = np.linspace(-2, 2, 100)
r = z**2 + 1
x = r * np.sin(theta)
y = r * np.cos(theta)

有了三个坐标轴的数据，就需要使用绘图函数来画出曲线，曲线的名称跟2D里是一样的，只是内部的对象发生了变化，并且3D里的函数也可以绘制2D曲线，只是参数传入几个来决定。

这里使用的函数定义如下：

Axes3D.plot(self, xs, ys, *args, zdir='z', **kwargs)

xs：X轴的坐标数组，一维数组。
ys：Y轴的坐标数组，一维数组。
zs：Z轴的坐标值，可以是一个点，也可以是一维数组。
zdir：可选值：{‘x’, ‘y’, ‘z’}，默认：’z’，当绘制二维数据时，选择那一个作为Z方向。
**kwargs：它的取值与matplotlib.axes.Axes.plot是一样的。

通过下面的例子来演示这个函数的一般使用：

import numpy as np

from matplotlib import pyplot as plt
from mpl_toolkits import mplot3d

plt.rcParams['legend.fontsize'] = 10
fig = plt.figure()
ax = fig.add_subplot(1,1,1, projection = "3d")

#
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100)
z = np.linspace(-2, 2, 100)
r = z**2 + 1
x = r * np.sin(theta)
y = r * np.cos(theta)

ax.plot(x, y, z, label='parametric curve')
ax.legend()

plt.show()

接着下来修改Z轴只有一点的二维图像绘制，修改代码如下：

ax.plot(x, y, 1.0, label='parametric curve')

只是把上面的例子里z轴的值改为都等于1.0情况，绘图如下：

Matplotlib 绘制3D图像

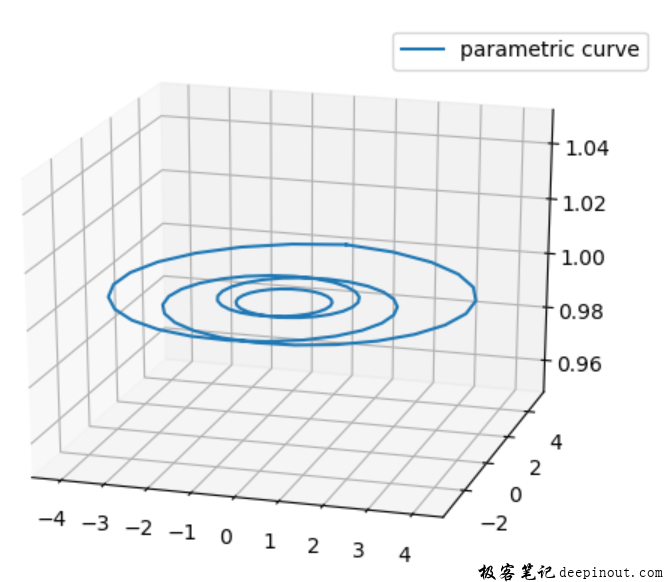
可以看到只有等于Z轴为1这个平面里绘制了数据。

通过上面的函数定义可以看到，默认是选择Z轴作为向上的深度的方向轴，如果有时候数据是选择X轴作为向上的方向轴，那么就需要作如下修改：

ax.plot(x, y, 1.0, label='parametric curve', zdir = 'x')

这时绘出图案与上面的图案就翻转了90度：

Matplotlib 绘制3D图像

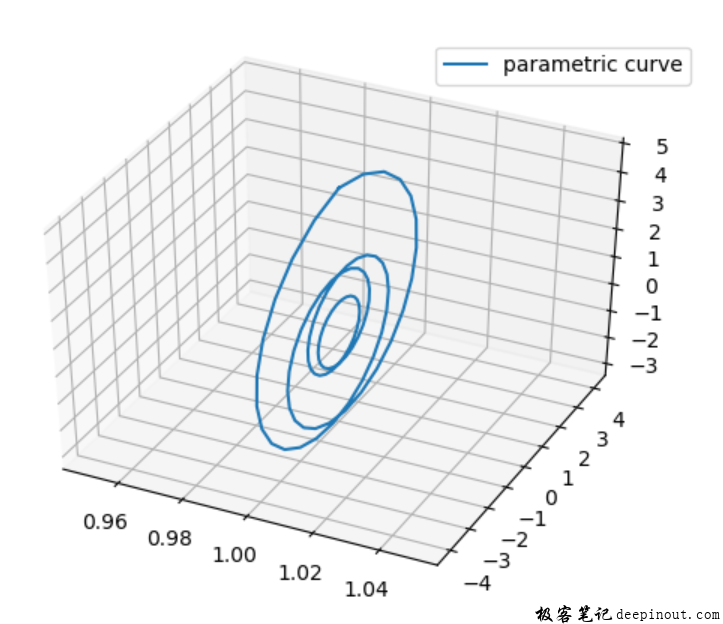
到这里就把这个三维的plot函数学习完成了。

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits import mplot3d

plt.rcParams['legend.fontsize'] = 10

fig = plt.figure()
ax = fig.add_subplot(1,1,1, projection = "3d")

#
theta = np.linspace(-4 * np.pi, 4 * np.pi, 100)
z = np.linspace(-2, 2, 100)
r = z**2 + 1
x = r * np.sin(theta)
y = r * np.cos(theta)

ax.plot(x, y, 1.0, label='parametric curve', zdir = 'x')
ax.legend()

plt.show()