Transfer Fcn：MATLAB中的传递函数

1. 引言

传递函数是系统控制工程中一个重要的概念，它用于描述线性时不变系统的输入与输出之间的关系。MATLAB作为一款功能强大的数学计算软件，在控制系统设计与分析中有着广泛的应用。本篇文章将通过详解Transfer Fcn在MATLAB中的使用方式，帮助读者更好地理解和应用传递函数。

2. 传递函数的基本概念

传递函数是用来描述线性时不变系统的输入和输出之间关系的数学模型。它可以对系统进行数学分析和仿真，帮助工程师设计和优化控制系统。在MATLAB中，传递函数通常使用Transfer Fcn对象进行表示。

传递函数的一般形式为：

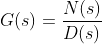
其中，N(s)和D(s)分别是分子多项式和分母多项式。传递函数的输入可以是连续时间的输入信号u(t)，输出是连续时间的输出信号y(t)。传递函数可以简化为以下形式：

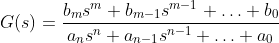
其中，m和n分别是分子多项式和分母多项式的次数，bm、bm-1、…、b0和an、an-1、…、a0分别是分子和分母多项式的系数。

3. MATLAB中的Transfer Fcn

在MATLAB中，我们可以使用transfer函数创建和分析传递函数。下面是transfer函数的基本语法：

sys = tf(num, den)

其中，num是分子多项式的系数，den是分母多项式的系数。sys是Transfer Fcn对象，代表传递函数。

通过transfer函数，我们可以进行传递函数的多种操作，例如计算传递函数的零点和极点、计算和绘制频率响应等。下面将介绍一些常用的操作。

3.1 计算传递函数的零点和极点

计算传递函数零点和极点是分析传递函数特性的重要步骤。在MATLAB中，我们可以使用zero和pole函数来实现。

例如，对于一个二阶传递函数，我们可以通过以下代码计算它的零点和极点：

sys = tf([1 2], [1 4 3]);
zeros = zero(sys)
poles = pole(sys)

运行结果如下所示：

zeros =

   -2

poles =

   -1
   -3

这里，零点为-2，极点为-1和-3。

3.2 计算和绘制传递函数的频率响应

传递函数的频率响应是描述系统对不同频率信号的传递特性。在MATLAB中，我们可以使用bode函数来计算和绘制传递函数的频率响应。

例如，对于一个二阶传递函数，我们可以通过以下代码计算和绘制它的频率响应：

sys = tf([1 2], [1 4 3]);
bode(sys)

这里，图中的横轴表示频率，纵轴表示幅值和相位。通过频率响应曲线，我们可以对系统的稳定性和频率特性有更深入的了解。

3.3 进行系统的仿真和响应分析

通过传递函数，我们可以进行系统的仿真和响应分析。MATLAB提供了一系列的函数来实现这些功能。

例如，我们可以使用step函数来计算并绘制系统的阶跃响应：

sys = tf([1 2], [1 4 3]);
step(sys)

这里，图中的横轴表示时间，纵轴表示系统的输出响应。通过阶跃响应曲线，我们可以对系统的稳定性和响应速度有更深入的了解。

4. 小结

本文详细介绍了MATLAB中的Transfer Fcn对象，以及它在传递函数建模和分析中的应用。我们学习了传递函数的基本概念和表示方法，并了解了如何通过MATLAB进行传递函数的各种操作，包括计算零点和极点、计算和绘制频率响应，以及系统的仿真和响应分析。

掌握MATLAB中Transfer Fcn的使用方法对于控制系统设计和分析非常重要。通过灵活应用Transfer Fcn对象，我们能够更好地理解和优化系统的动态特性，提高系统的性能和稳定性。